September 24th, 2019
LEARNING: in this class I learned that are the analog signals, digital and the different types of numerical systems that exist, likewise I learned to use each one and how it will serve me when we start to see more complicated programming languages, I hope in this period to learn more about computing and that I serve for my life more.
EXPLANATION : in class, our professor explained us how the matter was going to be in this period, additionally we made some consultations on analog, digital signals and the number system: (is the first thing we'll work on in the period):
What is an analog and an digital signal?
- an analog signal is generated by some type of electromagnetic phenomenon, which is represented by a continuous mathematical function of variable: amplitude period as a function of time.
- the digital signal is a signal that encodes signs to represent data in magnitudes of discrete values (a sequence of discrete values in binary could be: 0 0 1 1 1 0 1 1 1 0 1 0 1...
What are the binary, octal and hexadecimal system?
- Binary:a binary system is a numerical system represented with two digits: 0 and 1, is widely used in computers because only two voltages are used.
- Octal: is a positional numbering system based on the number 8, using Arabic Indian digits: 0,1,2,3,4,5,6,7. It has the advantage that it does not use other signs apart from digits
- Hexadecimal: is a positional numbering system based on the number 16, which means that there are 16 possible digit symbols. Their numbers are represented by the first 10 digits of the decimal numbering and the interval from number 10 to number 15 is represented by the letters of the alphabet: A, B, C, D, E and F.
conversions:
binary to decimal: To convert from binary to decimal, do the following:
Start on the right side of the binary number. Multiply each digit by 2 elevated to the consecutive power (starting with power 0.20).
After performing each of the multiplications, add them all and the resulting number will be the equivalent of the decimal system.
binary to octal: To convert from binary to octal, do the following:
- Group the binary quantity in groups of 3 by 3 starting on the right side. If at the end of grouping you do not complete 3 digits, then add leading zeros.
- Then see the corresponding value according to the table:
- Binary number 000 001 010 011 100 101 110 111
- Octal number 0 1 2 3 4 5 6 7
Example:
110111 (binary) = 67 (octal). Process
111 = 7
110 = 6
Group from left to right: 67
Binary to hexadecimal: To perform the binary to hexadecimal conversion, do the following:
- Group the binary quantity in groups of 4 to 4 starting from the right side. If when you finish grouping do not complete 4 digits, then add leading zeros.
- Then see the value that corresponds according to the table:
- Binary number 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
- Hexadecimal number 0 1 2 3 4 5 6 7 8 9 A B C D E F
3. The corresponding quantity in hexadecimal is grouped from right to left.
Examples
110111010 (binary) = 1BA (hexadecimal). Process
1010 = A
1011 = B
1 then add 0001 = 1
Group from right to left: 1BA
Decimal to binario: The number of the decimal system is divided by 2, whose whole result is then divided by 2, and so on until the dividend is less than the divisor, 2. That is, when the number to be divided is 1 the divisió ends
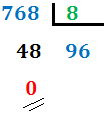
Decimal to octal: We divide the number by 8:
If the quotient is greater than or equal to 8, we divide it by 8.
In our case, the quotient is 96 (greater than 8), so we divide it again:
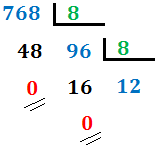
We go on like this until we get a quotient less than 8.
In our case, the quotient is 12 (greater than 8), so we divide it again:
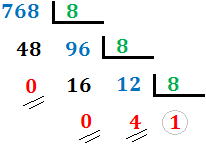
The quotient is 1, less than 8, so we have finished the process.
We have indicated the remains with two stripes and the last quotient with a circumference.
The number in base 8 is:
(Last quotient) (Last remainder) (Penultimate remainder)... (Second remainder) (First remainder).
In our case,
The last quotient is 1.
The last rest is 4.
The penultimate remainder is 0.
The first remainder is 0.
Therefore, the number 768 in octal base is 1400. That is
Decimal to hexadecimal: is done by dividing by 16 the decimal number we want to convert, treating the division as an integer division without decimals, note the rest and continue dividing the quotient obtained between sixteen to get a final quotient of between 1 and 15.
Achieving a sequence of decimal numbers with the remains of each division and the final quotient, which we substitute for the hexadecimal equivalent of the table above, and order them from right to left.
Example
247 (octal) = 010100111 (binary). The 2 in binary is 10, but in 3-bit binary is Oc(2) = B(010); the Oc(4) = B(100) and the Oc(7) = (111), then the binary number will be 010100111.
octal to decimal: In the decimal (base 10), each digit in octal is equal to that digit multiplied by the exponent of 8 that is equal to its location minus one.
Example: o3425 to decimal
|
Hexadecimal to decimal: Use the decimal value for each hexadecimal digit. For 0-9, it is the same, but A = 10, B = 11, C = 12, D = 13, E = 14, and F = 15.
Keep a sum of the numbers converted at each step below.
Start with the least significant hexadecimal digit. That is the digit on the right end. This will be the first item in a sum.
Take the second-least significant digit. That is next to the digit on the right end. Multiply the decimal value of the digit by 16. Add this to the sum.
Do the same for the third-least significant digit, but multiply it by 162 (that is, 16 squared, or 256). Add it to the sum.
Continue for each digit, multiplying each place by another power of 16. (4096, 65536, etc.)
|
When the quantity of bits in a binary numbers is not a multiple of 4, it is padded with zeros to make it so. Examples:
binary 110 = 0110, which is 6 Hex.
binary 010010 = 00010010, which is 12 Hex.
Hexadecimal to octal: The first step to convert a hexadecimal number into octal is to convert the hexadecimal number into binary, for this, we will help ourselves from the hexadecimal to binary converting table above and translate the hexadecimal number by writing below each digit the correspondence in binary.
Obtained the binary number we will make the conversion from binary to octal, starting by separating the binary number in blocks of 3 digits starting from the right to the left, we will take help from the table of binary conversion to octal that we have seen above and we will replace each block of binary digits by its corresponding equivalent in octal, in this way and so quickly you know how to convert a hexadecimal number to octal manually.
before finishing the class, professor christian showed us how to make a cardboard abacus and explained that we had to make one similar to the one he drew for the next class.





No comments:
Post a Comment